Uwaga metodologiczna: wszystkie rozważania w tym artykule dotyczą krzywych zerokuponowych. W celu otrzymania możliwości uwzględnienia obligacji kuponowych w krzywej zerokuponowej rozkładamy obligacje kuponowe na pęki obligacji bezkuponowych metodą bootstrapową. Zwiększa (zagęszcza) to znacząco liczbę punktów do aproksymacji.
Krzywa rentowności w pytaniach i odpowiedziach
Co na temat stóp procentowych można znaleźć w serwisie InvestTracer?
Jak wykorzystać krzywą rentowności w praktyce?
Krzywa rentowności w pytaniach i odpowiedziach
Czym jest struktura terminowa stóp procentowych?
Struktura terminowa stóp procentowych opisuje zależność między terminem wykupu instrumentu wolnego od ryzyka (np. obligacji rządowej lub bonu skarbowego), a oferowaną przez ten instrument rentownością. Innymi słowy struktura terminowa stóp procentowych opisuje stopy zwrotu wolne od ryzyka dla różnych terminów inwestycji.
Co to są stopy procentowe spot i forward oraz struktura terminowa forward?
Stopy spot to bieżące stopy procentowe, czyli stopy dla okresów zaczynających się teraz i kończących się w danym momencie w przyszłości. Odzwierciedla je zbiór krzywych dochodowości. W przeciwieństwie do nich stopy rynku terminowego (stopy forward) to stopy dla przyszłych okresów – zaczynających i kończących się w przyszłości (ale stopy te są ustalone już teraz). Innymi słowy stopy forward określają, z jakimi odsetkami mogą być dokonywane w danej chwili przyszłe reinwestycje. Graficznie odzwierciedla je zbiór krzywych terminowych.
Dlaczego potrzebne jest estymowanie struktury terminowej?
Dlaczego przydatna jest znajomość rentowności r(t) dla dowolnego momentu t? Powody są co najmniej dwa.
- Obserwowane ceny obligacji mogą się różnić od „prawdziwych” (fundamentalnych) cen z powodu istnienia „szumu” rynkowego. Szacując stopy procentowe spot dla różnych okresów, chcemy – o ile to możliwe – wyeliminować wpływ zakłóceń. Estymacja ciągłej struktury zapewnia wygładzenie oszacowań. Stopa r(t) dla dowolnego momentu t jest uśredniana ze stopami procentowymi dla momentów sąsiednich, dzięki czemu zmniejsza się wpływ szumu.
- Drugim istotnym powodem jest to, że w wielu modelach teoretycznych zakłada się znajomość ciągłej struktury terminowej. Jest ona potrzebna np. do obliczania pewnych miar ryzyka, prognozowania zmienności cen obligacji lub stóp procentowych czy do wyceny instrumentów pochodnych.
Co to jest metoda Svenssona i dlaczego się ją stosuje?
Metoda Svenssona jest jedną z metod wyznaczania (estymacji) krzywej dochodowości. Wyznaczana tą metodą krzywa jest gładka, giętka i stabilna.
Istotną cechą metody Svenssona jest to, że posiada mocne podstawy teoretyczne. W jej przypadku przyjęto następujące założenia:
- Istnieje stopa krótkookresowa i długookresowa (obligacji konsolowej, czyli wieczystej - nie podlegającej wykupowi).
- W miarę wydłużania się terminu zapadalności stopy procentowe stopniowo zbliżają się do poziomu stopy długookresowej
- Dla średnich okresów na krzywej dochodowości może wystąpić jeden lub dwa garby (dołki).
- Ponadto w metodzie tej występuje mała liczba parametrów, które, co istotne, mają naturalną interpretację.
Interpretacja parametrów krzywej Svenssona
- b0 odpowiada za kształt krzywej dla długich terminów zapadalności. Jest to stopa, do której krzywa dąży w nieskończoności,
- b1 odpowiada za kształt krzywej dla najkrótszych terminów zapadalności,
- Suma b0 + b1 jest interpretowana jako bieżąca stopa oprocentowania lokaty overnight,
- -b1, czyli parametr ze znakiem ujemnym odpowiada tzw.spreadowi krzywej, czyli różnicy długoterminowej i krótkoterminowej stopy procentowej.
Przykład Spreadu dodatniego (normalna krzywa dochodowości):
Ujemny spread krzywej (odwrócona krzywa dochodowości) występuje, gdy rentowności długoterminowe są mniejsze niż krótkoterminowe (nachylenie krzywej jest odwrotne do prezentowanego wyżej). Taka sytuacja najczęściej występuje przy wysokim, ale malejącym poziomie stóp procentowych i wysokiej, ale malejącej inflacji. W Polsce miała miejsce jeszcze w latach 1999 -2003. Obecnie krzywa ma kształt uznawany za normalny, co świadczy o względnej stabilizacji sytuacji finansowej i gospodarczej.
- b2 odpowiada za kształt środkowego odcinka krzywej, w tym za istnienie ewentualnego garbu (dołka) krzywej,
- b3 podobnie jak b2, przy czym umożliwia dodanie drugiego garbu (dołka), a więc zwiększa elastyczność i poprawia dopasowanie krzywej do danych,
- ilorazy b1/b2 i b1/b3 odpowiadają za rodzaj dwóch możliwych ekstremów krzywej (garb, czy dołek),
- t1 determinuje wartość czasu zapadalności, dla którego funkcja osiąga pierwsze ekstremum (garb lub dołek),
- t2 determinuje wartość czasu zapadalności, dla którego funkcja osiąga drugie ekstremum (garb lub dołek).
Poniżej przykład opisu krzywej dochodowości równaniem Svenssona:

Ważne!
Pod każdym dziennym wykresem krzywej dochodowości w serwisie InvestTracer podajemy jej równanie wraz z wartościami parametrów. Przedstawiamy też krótką interpretację kształtu krzywej według trzech podstawowych teorii opisujących strukturę terminową. Powinno to ułatwić zrozumienie aktualnej sytuacji na rynku obligacji skarbowych.
Jakie są najpopularniejsze zastosowania terminowej struktury stóp procentowych?
Najbardziej znane zastosowania to:
- wycena papierów wartościowych niezależnie od struktury oferowanych przez nie płatności. W szczególności możliwe staje się porównywanie ze sobą obligacji o identycznych terminach wykupu, ale różniących się konstrukcją i wielkością kuponu. Ponadto porównując rzeczywiste stopy dochodowości (a więc wyceny) poszczególnych obligacji dostępnych na rynku z wycenami teoretycznymi (z ciągłej krzywej dochodowości) można określić papiery przewartościowane (pod krzywą) i niedoszacowane (nad krzywą), co pozwala dokonać korzystnych inwestycji.
- prognozowanie stóp procentowych - poprzez wyliczenie ze struktury spot struktury forward, czyli implikowanych krzywych terminowych. Krzywe terminowe odzwierciedlają bowiem aktualne oczekiwania co do kształtowania się stóp procentowych w przyszłości.
- opis niektórych zjawisk w gospodarce realnej (tempo wzrostu gospodarczego, restrykcyjność polityki pieniężnej, popyt i podaż długoterminowych instrumentów dłużnych i kredytu długoterminowego, związanego z popytem inwestycyjnym ze strony przedsiębiorstw).
- prognozowanie inflacji za pomocą równania Fishera.
Co opisuje równanie Fishera?
Równanie Fishera (równanie wymiany Fishera) – zależność pomiędzy ilością pieniądza w gospodarce i poziomem cen.
Irving Fisher jako pierwszy rozróżnił nominalną i realną stopę procentową proponując równanie, nazwane później jego imieniem.
![]()
i = nominalna stopa procentowa
Kiedy inflacja jest na niskim poziomie, realne stopy procentowe mogą być przybliżone wartością nominalnej stopy procentowej minus tempo inflacji.
Co to jest dP/P i po co się je wyznacza?
dP/P oznacza procentową zmianę ceny danej obligacji w reakcji na wzrost stopy procentowej o jeden punkt procentowy. Oznacza zatem wrażliwość ceny obligacji na zmiany stopy procentowej. Jest uważany za miarę ryzyka inwestowania w daną obligację. Dla obligacji o takim samym czasie do wykupu mniej ryzykowna będzie zatem ta, która jest mniej wrażliwa na zmianę stopy procentowej.
Co to jest czas trwania obligacji i do czego służy?
Czas trwania (ang. Duration), jest powszechnie stosowaną miarą wrażliwości zmian ceny obligacji na zmiany stopy procentowej. Zgodnie ze swoją nazwą, Duration oznacza średni ważony okres oczekiwania na wpływy środków pieniężnych z obligacji.
Duration obligacji jest zazwyczaj równa jej liczbie lat do wykupu (w przypadku obligacji zerokuponowych) lub od niej mniejsza (w przypadku obligacji płacących odsetki). Ponadto, obligacje płacące wyższe odsetki mają mniejszą duration, ponieważ większa część środków jest wypłacana w formie kuponu, czyli krótszy jest czas oczekiwania na zwrot zainwestowanych środków.
Duration, to średni czas życia danej inwestycji ważony udziałem wartości obecnej kolejnych przepływów gotówki w wartości obecnej całej inwestycji:
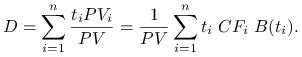
Natomiast Convexity (wypukłość), to średni kwadrat czasu życia danej inwestycji:

gdzie:
D – duration
C – convexity
CFi – nieujemny przepływ gotówki w chwili Ti
PVi – wartość bieżąca i-tego przepływu gotówki

gdzie:
PV – wartość bieżąca inwestycji (Present Value)
Ti – czas, po którym nastąpi i-ty przepływ gotówki CFi.
B(Ti) - Czynnik dyskontujący, odwrotność rentowności dla czasu Ti, B(Ti)=1/r(Ti)
Duration wraz z Convexity (wypukłością) służą do obliczania zmian cen obligacji w zależności od zmian poziomu stóp procentowych (dP/P). Ponadto bywa używana przez zarządzających portfelami obligacji jako miara ryzyka związanego z inwestowaniem w daną obligację. Pomaga zatem w doborze składników do portfela obligacji.
Do czego stosuje się Convexity?
Convexity, czyli wypukłość służy wraz z Duration do obliczania zmian cen obligacji w zależności od zmian poziomu stóp procentowych (dP/P).Powiązania zmian cen obligacji ze zmianami poziomu stóp procentowych nie mają charakteru liniowego. Stosowanie tylko miary Duration do obliczenia tej zmiany nie dają więc dokładnego wyniku. Im większa zmiana stopy procentowej tym różnica pomiędzy otrzymanym wynikiem a rzeczywistą zmianą jest większa. W celu dokładniejszego obliczenia zmiany wartości obligacji stosujemy dodatkowo miarę Convexity, czyli wypukłość obligacji.
Co na temat stóp procentowych można znaleźć w serwisie InvestTracer?
W portalu InvestTracer.com znajduje się dział poświęcony stopom procentowym i obligacjom skarbowym. W ramach tej części serwisu udostępniane są:
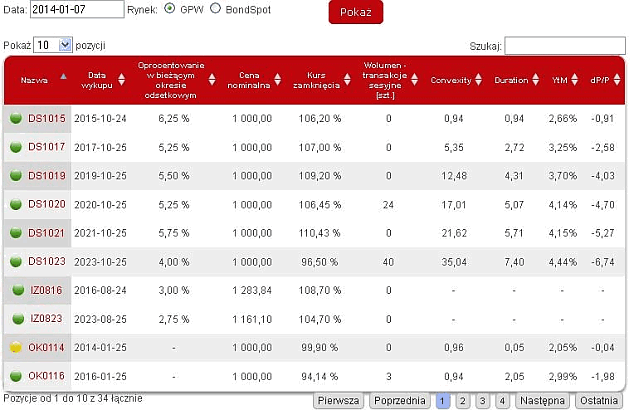
- aktualne ceny, stopy YTM, a także duration i convexity dla obligacji skarbowych
- krzywa dochodowości wyznaczana na podstawie notowań papierów skarbowych z GPW i z rynku BondSpot,
- informacje o emisjach obligacji Skarbu Państwa,
- rentowność w czasie, czyli struktura czasowa rynku obligacji.
Struktura terminowa rynku obligacji opisuje zależność między terminem do wykupu instrumentu wolnego od ryzyka (na przykład obligacji rządowej lub bonu skarbowego) a dochodowością (rentownością). Innymi słowy struktura terminowa opisuje stopy zwrotu wolne od ryzyka dla różnych terminów inwestycji. Aktualna struktura terminowa rynku obligacji skarbowych opisana została liczbowo w formie tabeli oraz graficznie w postaci krzywej dochodowości (rentowności). Tabela zawiera dane niezbędne do bieżącej analizy i monitorowania rynku, z możliwością ich sortowania.
Odrębna zakładka zawiera szczegółowe informacje na temat wybranej obligacji:

Krzywa dochodowości obrazuje w sposób ciągły zależność między terminem do wykupu obligacji a dochodowością (rentownością) na dany dzień.
Struktura terminowa rynku obligacji dostępna jest z poziomu menu głównego Analiza obligacji.
Jak wykorzystać krzywą rentowności w praktyce?
Przykładowa procedura doboru obligacji do portfela aktywnie zarządzanego może wyglądać następująco: na krzywej obligacji prezentującej strukturą czasową rynku obligacji znajdujemy przebiegi rentowności w czasie dla zadanych czasów do wykupu. Stwierdzamy, że dla czasów krótkich (na przykład 6 miesięcy do 1 roku) rentowności spadają, co oznacza, że ceny obligacji z tego fragmentu krzywej dochodowości rosną. Ponadto obserwujemy, że dla średnich i długich okresów do wykupu (3 lata i więcej) rentowności rosną, czyli ceny obligacji spadają.
Na podstawie tych obserwacji stwierdzamy, że będą nas interesowały obligacje o czasie do wykupu od kilku miesięcy do 3 lat. W tym zakresie czasowym (fragment krzywej wybrany do tworzenia portfela, zaznaczony na wykresie poniżej) dokonamy wyboru obligacji.
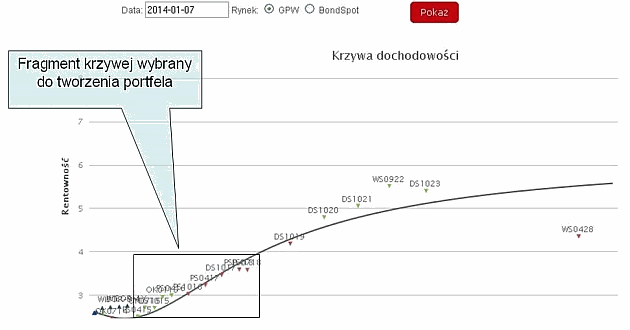
Spośród obligacji znajdujących się na wybranym fragmencie krzywej preferujemy te, które widnieją ponad krzywą (ich rentowności są większe, zatem są niedoszacowane, w przeciwieństwie do obligacji znajdujących się poniżej krzywej – przeszacowanych). Ta preferencja ma szczególne uzasadnienie, gdy odległości obligacji od krzywej są duże, co sugeruje szczególnie atrakcyjne papiery (lub przeciwnie – mniej interesujące).
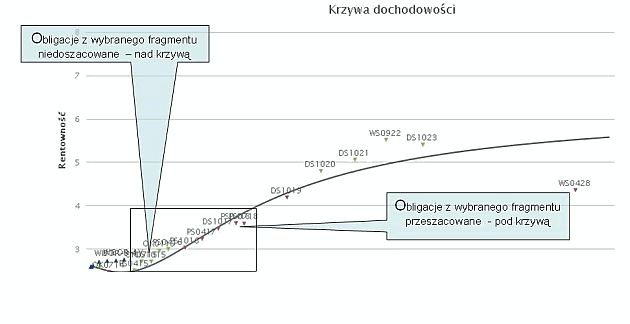
Ryszard Łukoś, www.InvestTracer.com